CYBERNÉTIQUE - Principe

CYBERNÉTIQUE - Principe

Norbert Wiener définissait la cybernétique comme l’«étude de la commande et de la communication chez l’animal et dans la machine». Les progrès accomplis dans les domaines de l’automatique et de l’informatique ont conduit à adopter une définition plus générale: la cybernétique est l’étude des systèmes considérés sous l’angle de la commande et de la communication. Dans cette définition, un système est un ensemble de phénomènes et d’événements interdépendants que l’on extrait du monde extérieur par une démarche intellectuelle arbitraire, en vue de traiter cet ensemble comme un tout. Les actions du monde extérieur sur le système se traduiront par l’existence de «variables de sortie».

Si l’on considère, par exemple, un ensemble de cinq événements ou phénomènes dont les relations d’interdépendance sont matérialisées par des flèches, on définit, sur cet ensemble, un certain nombre de systèmes (fig. 1).

Le point de vue nouveau introduit par la cybernétique tient à ce que les variables d’entrée et de sortie peuvent être non seulement des actions au sens mécanique du terme, mais encore des informations.

1. Définition des systèmes

L’étude d’un système consiste, une fois que ses variables d’entrée et de sortie ont été définies, à rechercher les relations fonctionnelles qui existent entre ces variables, c’est-à-dire à établir un modèle mathématique du système. Pour ce faire, on est amené à introduire un certain nombre de variables auxiliaires qui ne dépendent que du système et que l’on appelle les variables d’état.

Si x ¹, x ²,..., x ^p sont les variables d’entrée, y ¹, y ²,..., y ^q les variables d’état et z ¹, z ²,..., z ⁿ les variables de sortie, on peut considérer les x ⁱ comme les composantes d’un vecteur d’entrée X (t ) (t représentant le temps), les y ⁱ comme les composantes d’un vecteur d’état Y (t ) et les z ⁱ comme les composantes d’un vecteur de sortie Z (t ).

Avec les notations ci-dessus, on peut dire que l’étude d’un système vise à l’obtention sous forme explicite de deux équations:

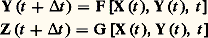La première d’entre elles est l’équation de transition qui décrit comment le système évolue dans le temps, tandis que la seconde est l’équation d’action qui décrit comment se déroule dans le temps l’action du système sur le monde extérieur.

Une approche aussi générale permet de décrire le comportement d’un système en faisant totalement abstraction de la nature (physique, chimique, biologique, etc.) des phénomènes étudiés. Elle permet, par conséquent, d’étudier certaines propriétés des systèmes, indépendamment de leur mode de réalisation (invariance temporelle, stabilité, linéarité, etc.).

L’étude générale des propriétés des systèmes permet également de définir des classes de systèmes , en réunissant dans une même classe tous les systèmes qui ont en commun un certain nombre de propriétés (systèmes asservis, adaptatifs, autodidactes, etc.).

Comme, par ailleurs, l’ensemble des propriétés caractéristiques d’une classe ne peut être obtenu que par une structure particulière du système (existence d’une ou plusieurs boucles de retour pour les systèmes asservis, existence d’une mémoire contenant un modèle pour les sytèmes adaptatifs, etc.), il en résulte que tous les systèmes d’une même classe ont non seulement des propriétés communes, mais encore, et c’est là le point important, une structure commune.

Dans ces conditions, si l’étude d’un système particulier permet d’affirmer sans ambiguïté qu’il appartient à une classe déterminée de systèmes, on peut en déduire immédiatement un certain nombre de conclusions quant à sa structure et chercher, par conséquent, comment cette structure est mise en œuvre (procédés chimiques, physiques, etc.) dans le cas particulier du système étudié.

Cette démarche est caractéristique de la cybernétique et l’on voit qu’elle peut s’appliquer à n’importe quel domaine, mais il est clair que c’est dans le cas des systèmes très complexes qu’elle apportera le plus souvent un point de vue original (biologie, physiologie, psychologie, sociologie, etc.).

2. Théorie des automates

Systèmes d’automates

On va essayer de montrer les démarches de la cybernétique en se limitant aux «systèmes discrets», c’est-à-dire aux automates encore appelés «automates d’états finis».

Un automate est, par définition, un quintuplet:

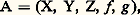où X est l’ensemble fini des symboles d’entrée, Y l’ensemble fini des états, Z l’ensemble fini des symboles de sorties, f une application de X 憐 Y dans Y, et g une application de X 憐 Y dans Z.

Un automate est complètement défini lorsqu’à tout couple (symbole d’entrée-état), on sait faire correspondre un état appelé «état suivant» et un symbole de sortie. Un tel automate est un automate de Mealy, alors que dans un automate de Moore le symbole de sortie ne dépend que de l’état et ne dépend pas du symbole d’entrée. Un automate est donc un système abstrait qui, à toute suite ordonnée de symboles pris dans l’ensemble X, fait correspondre une suite ordonnée de symboles pris dans l’ensemble Z; pour établir les relations qui existent entre ces deux suites, on est amené à introduire des symboles auxiliaires, appelés états, qui seront, par définition, des éléments d’un ensemble Y. Dans le cadre de la théorie des automates, il n’y a pas lieu d’attacher aux termes «symbole d’entrée», «symbole de sortie» et «état» d’autre signification que celle qui découle de la définition ci-dessus. L’intérêt de la notion d’automate vient de ce qu’elle permet une formalisation de la notion de système et, par conséquent, une étude des propriétés générales de ceux-ci, indépendamment de leur mode de réalisation.

Représentation d’un automate

Le mode de représentation usuel est un tableau dans lequel on explicite les applications f et g . Pour l’automate du tableau 1, on a:

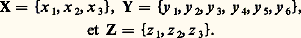La colonne de gauche indique l’état dans lequel se trouve l’automate et les différentes colonnes indiquent dans quel état il passe pour chacun des symboles d’entrée; enfin, la colonne de droite indique le symbole de sortie en fonction de l’état (automate de Moore); on voit, par exemple, que si l’automate est dans l’état y ⁵ et qu’il reçoit le symbole x ², alors il passe dans l’état y ¹ et délivre le symbole z ³.

Image homomorphe d’un automate

Un automate A¹ = (X¹, Y¹, Z¹, f ¹, g ¹) est une image homomorphe d’un automate A = (X, Y, Z, f , g ) si, et seulement si, il existe trois applications surjectives:

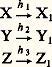telles que:

avec x 捻 X et y 捻 Y.

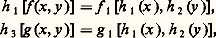Si les trois applications sont bijectives, alors A¹ et A sont isomorphes , c’est-à-dire qu’ils sont identiques, sauf en ce qui concerne les noms des symboles d’entrée, des symboles de sortie et des états.

Si nous considérons la machine de la figure 2, celle-ci est une image homomorphe de la machine du tableau 1 par les trois applications h ¹, h ², h ³ définies sur la figure 2. On aura, par exemple:

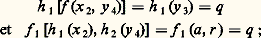ainsi que:

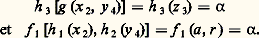Si deux chercheurs A et B proposent respectivement les automates du tableau 1 et de la figure 2 pour expliquer le fonctionnement d’un système, ils auront raison tous les deux, mais le chercheur B aura laissé échapper certains faits significatifs qui lui auraient permis de voir qu’il y a trois symboles d’entrée distincts, trois symboles de sortie distincts et six états. L’analyse du chercheur A a été plus fine et lui a permis d’aboutir à un modèle plus précis.

De la même manière, si, en étudiant deux systèmes quelconques, on trouve pour le premier un automate qui est une image homomorphe de l’automate du second, on pourra dire que le premier système est une forme simplifiée du second quelle que soit par ailleurs la nature de chacun de ces deux systèmes.

Automates équivalents et automate minimal

Considérons deux automates A¹ et A² ayant le même ensemble de symboles d’entrée et le même ensemble de sortie, mais des ensembles d’états différents, Y¹ et Y².

Un état y ^{i 1} 捻 Y¹ et un état y ^{j 2} 捻 Y² seront dits équivalents si, en appliquant la même suite de symboles d’entrée à l’automate A¹ placé initialement dans l’état y ^{i 1} et à l’automate A² placé initialement dans l’état y ^{j 2}, on obtient exactement la même suite de symboles de sortie pour A¹ et pour A².

Dans ces conditions, deux automates A¹ et A² seront équivalents si, pour tout état y ^{i 1} de A¹, il existe un état y ^{j 2} de A² qui lui soit équivalent, et si, pour tout état y ^{p 2} de A², il existe un état y ^{q 1} de A¹ qui lui soit équivalent.

Il résulte de cette définition que deux automates équivalents sont deux automates que l’on ne peut distinguer l’un de l’autre, puisque, à une même suite de symboles d’entrée, chacun d’eux répond par la même suite de symboles de sortie.

Cette relation d’équivalence entre deux états s’applique évidemment aux états d’un même automate, et, comme cette relation est une relation d’équivalence au sens strict (symétrique, réflexive et transitive), il en résulte qu’elle entraîne une partition de l’ensemble des états de l’automate. Il existe alors un homomorphisme qui fait correspondre à chacun des états d’une classe d’équivalence de l’automate initial un seul et même représentant de cette classe. L’image homomorphe de l’automate initial est alors un nouvel automate, appelé automate réduit, qui est équivalent au premier par définition, comporte un nombre moindre d’états et, de plus, est unique (à un isomorphisme près).

Dans ce cas particulier, l’automate réduit n’est pas une «version simplifiée» de l’automate initial, comme on l’a vu précédemment, mais un automate dans lequel on a réduit le nombre d’états au strict minimum.

Ainsi, l’automate du tableau 3 est l’automate minimal de l’automate du tableau 2, avec l’homomorphisme

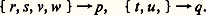On pourrait dire, dans ce cas, que l’automate du tableau 2 est inutilement compliqué, puisque celui du tableau 3 peut avantageusement jouer le même rôle.

Décomposition des automates

Un aspect important de la théorie des automates est l’étude de leur structure. Un automate étant donné, on peut en effet se demander s’il est ou non réalisable à l’aide de sous-automates convenablement reliés entre eux. Les deux modes de décomposition les plus simples sont les décompositions en série et en parallèle, conformément aux figures 3 et 4.

Cela revient évidemment, dans l’étude d’un système, à chercher si ce système est décomposable en sous-systèmes plus ou moins indépendants, mais alors que cette étude est difficile dans le cas des systèmes où l’approche est nécessairement empirique, elle est relativement facile pour les automates, car il suffit alors de chercher s’il existe une ou plusieurs structures algébriques sur l’ensemble des états.

On appelle «partition avec propriété de substitution» de l’ensemble des états d’un automate toute partition telle que, pour tout symbole d’entrée, les successeurs de deux états pris dans un même sous-ensemble appartiennent tous deux à un même sous-ensemble de cette partition.

Pour l’automate du tableau 4, on voit, par exemple, que 1, 2, 3 et 4, 5, 6 forment une partition avec propriété de substitution (les successeurs de 2 et 3 sont les états 4 et 5 pour le symbole 0 et les états 2 et 3 pour le symbole 1; or on a bien 4 et 5 捻 4, 5, 6 et 2 et 3 捻 1, 2, 3, etc.).

L’existence de partitions avec propriété de substitution entraîne la possibilité de décomposition de l’automate; la décomposition étant d’autant plus poussée que le nombre de ces partitions est plus élevé.

Enfin, l’introduction de l’algèbre des paires de partition permet de montrer que certains automates décomposables ne sont pas réalisables sans boucle de retour (fig. 5). L’existence de cette classe d’automates présente un grand intérêt, car ils ont un comportement en quelque sorte «pathologique».

Considérons, en effet, un automate qui, à un instant déterminé, présente une «défaillance», c’est-à-dire qui commet une erreur transitoire. Cela se traduira par le passage d’un état p à un état s , au lieu d’un passage à l’état q , à la suite de quoi le passage d’un état au suivant redevient normal, c’est-à-dire conforme à la table qui définit l’automate.

Dans ces conditions, le comportement de l’automate (relation entre les symboles d’entrée et de sortie) est perturbé pendant un temps dont la durée dépend de la structure de l’automate.

On montre, en particulier, que si l’automate est décomposable sans boucle de retour, les conséquences de l’erreur transitoire sont toujours éliminées en un temps fini, alors que, dans le cas contraire, le comportement reste définitivement perturbé, c’est-à-dire que les conséquences de défaillance transitoire ne sont jamais éliminées. L’analogie avec le comportement pathologique de certains systèmes biologiques est ici particulièrement frappante.La cybernétique s’attache à l’étude des systèmes sur un plan très général. Elle a pour objet de mettre en évidence les propriétés de ces systèmes, indépendamment de leur nature physique. Cette démarche, propre à la cybernétique, développée dans le cas des systèmes discrets, peut, bien sûr, s’appliquer aux systèmes continus, mais les problèmes dans ce domaine sont nettement plus complexes et font l’objet de très nombreux travaux.

Encyclopédie Universelle. 2012.